 |
|---|
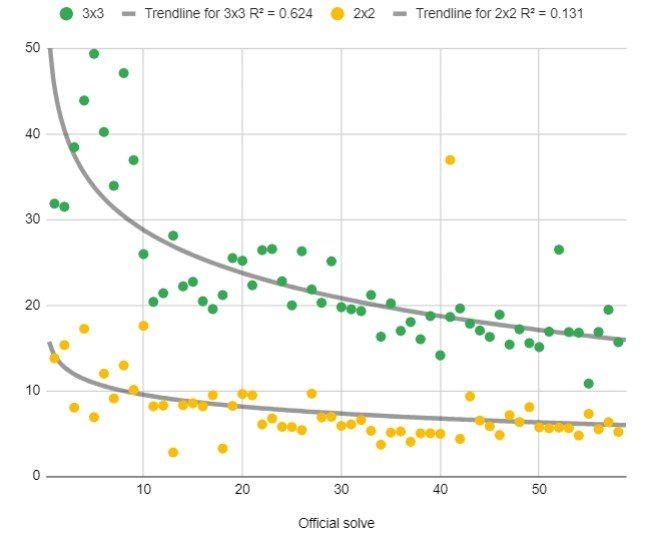
Analyzing the drop-off points in the data:
3x3
The first major drop-off in 3x3 times occurred after the 10th solve. This is due to a several month gap between the previous solves and the solves that came after. During this gap, I had learned some slightly more advanced sets of cube-solving algorithms such as F2L, 2-Look OLL, and 1-Look PLL; the specifics of each algorithm set are not that relevant to this report, but they drastically improved my solving times.
The second major drop-off in 3x3 times occurred between the 29th and 30th solves, which were separated by a two-year gap thanks to the pandemic. During this time, I had begun learning more advanced solving algorithms such as the 1-Look OLL set, as well as improving my execution of other algorithms. Additionally, I also achieved full colour neutrality, which is the ability to begin solving a cube from any side of your choosing, instead of having to begin from the same side every time.
2x2
The first major drop-off in 2x2 times occurred within the same several month gap as the first major drop-off in 3x3 times. My times here improved thanks to the same 2-Look OLL algorithm set that I learned for 3x3.
The second major drop-off in 2x2 solving times occurred between the 21st and 22nd solves. In the interval between those, I had learned an entirely new solving method specifically for 2x2, known as the Ortega method which allowed for much more efficiency in solving.
The third major drop-off in 2x2 times occurred at the same time as the second 3x3 one, after the pandemic. I did not learn many new things for 2x2 during the pandemic, so the drop-off there is primarily caused by full colour neutrality much like with 3x3.
Extrapolation
Assuming that the current trends will continue, we can extrapolate that by the 100th official solve, the time for 2x2 will not improve by much, but there will be a definite improvement in 3x3 solving times.